DeepSeek researchers have unveiled a significant architectural advancement for large language models, introducing a technique called Manifold-Constrained Hyper-Connections, or mHC, designed to resolve a long-standing trade-off between a model's expressiveness and the stability of its training process. This innovation, which employs a rigorous mathematical constraint, addresses the fundamental problem of information flow in highly expanded network architectures, potentially unlocking the next generation of scalable foundation models. The technique offers a new pathway for the AI industry to achieve higher performance and better reasoning capabilities without resorting to unsustainable brute-force scaling.

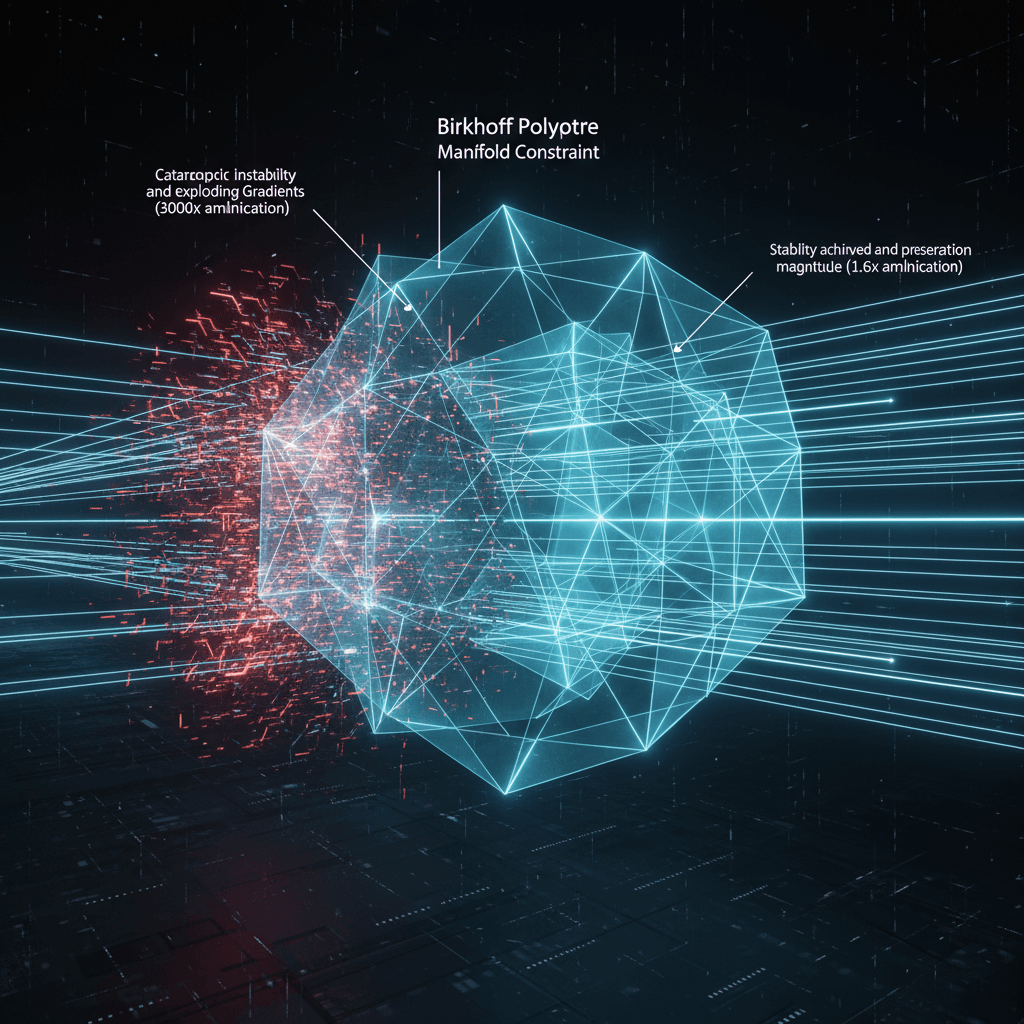
The core of the issue lies in the design of residual connections, the 'skip connections' that have been an integral part of deep learning since the ResNet architecture was introduced nearly a decade ago. Residual connections allow information to bypass layers, ensuring that the signal magnitude remains stable and gradients can flow easily backward through the deep network during training. This identity mapping property is crucial for training models with hundreds of layers, preventing the training error from paradoxically increasing with model depth. However, as models scaled to billions of parameters, researchers began experimenting with Hyper-Connections (HC), which extend the single residual stream into multiple parallel data streams, or 'highways,' managed by learnable mixing matrices. While this approach dramatically increases the model's learning capacity and flexibility, empirical results showed a catastrophic failure mode in large-scale training, such as in a 27-billion-parameter model where the unconstrained composite mappings caused signal amplification to exceed 3000 times, leading to a sudden and complete loss of stability, often resulting in exploding gradients and training divergence.[1][2][3][4][5][6]

DeepSeek's Manifold-Constrained Hyper-Connections directly address this instability by imposing a geometric constraint on the learnable mixing matrices. Specifically, the mHC framework forces these connection matrices onto the Birkhoff Polytope, a mathematical manifold that defines the space of all doubly stochastic matrices—matrices where every row and every column sums to 1.0. This constraint is mathematically elegant because the property of double stochasticity guarantees signal magnitude preservation, ensuring that as information passes through a layer, the total 'mass' of the signal remains constant. Crucially, the set of doubly stochastic matrices is closed under matrix multiplication, meaning that even when stacking hundreds of layers, the composite mapping across the entire network is guaranteed to maintain this stability property. This structural safeguard is the key to decoupling model capacity from training instability. The researchers leverage the classic Sinkhorn-Knopp algorithm, an iterative normalization method, to project the learned matrices onto this manifold, ensuring the constraint is met in a computationally feasible way during training.[1][2][3][4][5][6]

The empirical results from DeepSeek's experiments validate the effectiveness of mHC across various model scales, including 3 billion, 9 billion, and a critical 27-billion-parameter model, often based on a Mixture-of-Experts (MoE) architecture. For the 27B model, where unconstrained Hyper-Connections failed catastrophically with loss spikes and wild gradient behavior, the mHC architecture maintained a smooth training loss curve throughout the entire process. The maximum signal amplification factor, which reached 3000x in the unconstrained setup, was dramatically reduced and controlled to a stable 1.6x with mHC. This restored stability is not just a training convenience; it translates directly into significant performance gains. Models trained with mHC showed marked improvements on complex reasoning benchmarks, with one set of experiments demonstrating an improvement of over seven percentage points in accuracy on the BIG-Bench Hard (BBH) test, which is a key measure of multi-step reasoning. Importantly, these substantial gains in performance and stability came with a marginal computational cost, adding only about a 6.7% overhead to the total training time, a figure the researchers deemed negligible for large-scale foundational model development.[1][2][3][7][5][8][6][9]

The implications of this breakthrough for the broader AI industry are profound, suggesting a potential shift away from purely increasing parameter counts and toward architectural optimization. The mHC technique addresses a fundamental constraint that has limited innovation in transformer-based architectures for years, demonstrating that stability and expressiveness do not have to be a zero-sum trade-off. By allowing for the stable use of expanded connection topologies, mHC opens the door for building AI models that can process information with higher bandwidth and more complex internal routing, leading to a more efficient utilization of computational resources. The technique also offers a more reliable and cost-effective method for training, minimizing the waste of compute resources associated with catastrophic training failures, a critical concern as training runs become more expensive and time-consuming. Co-authored by DeepSeek's founder, the paper signals the company's intent to integrate mHC into its next generation of flagship models, positioning the Chinese AI firm at the forefront of architectural innovation and providing a competitive edge in the global race to develop more intelligent and scalable foundation models.[1][3][7][10][11][12][9]